Three point Bending formula for Rectangular , Circular, square and hollow sections

Three point bending test is used for determination of Modulus of Elasticity of a material (E) , Bending stress (σ_y) / Flexural stress of material or Flexural strain . The result obtained might be different depending upon the shape and size of material and the loading condition .

Three point bending means there occurs bending due to load or forces acting on three different point along the length of a testing specimen. In this article , we will be dealing with the three point bending formula for different sections like rectangular, circular , square etc.

Three point Bending Formula for Rectangular Section

Consider a rectangular section of a simply supported beam beam having length (l) , breadth (b) , and depth (d) . Whose Modulus of Elasticity is E and Bending stress σ_y. A point load (P) is applied at the center of this simply supported rectangular beam at the middle span as shown in the figure below.

 

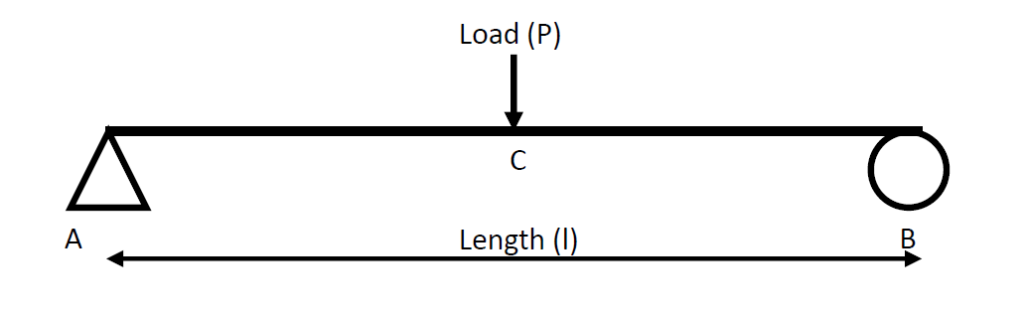
As the load is acting on the center of the beam , there will be two equal and opposite reactions acting from two supports at point A and B. By this, there will be total of three forces acting on the beam (i.e. R_A,R_B and load P ) and R_A=R_B=P/2 .

Maximum bending moment will occur at the center of the beam which will be equal to P/2*l/2 = Pl/4 as shown in the bending moment diagram of this beam in the figure below.

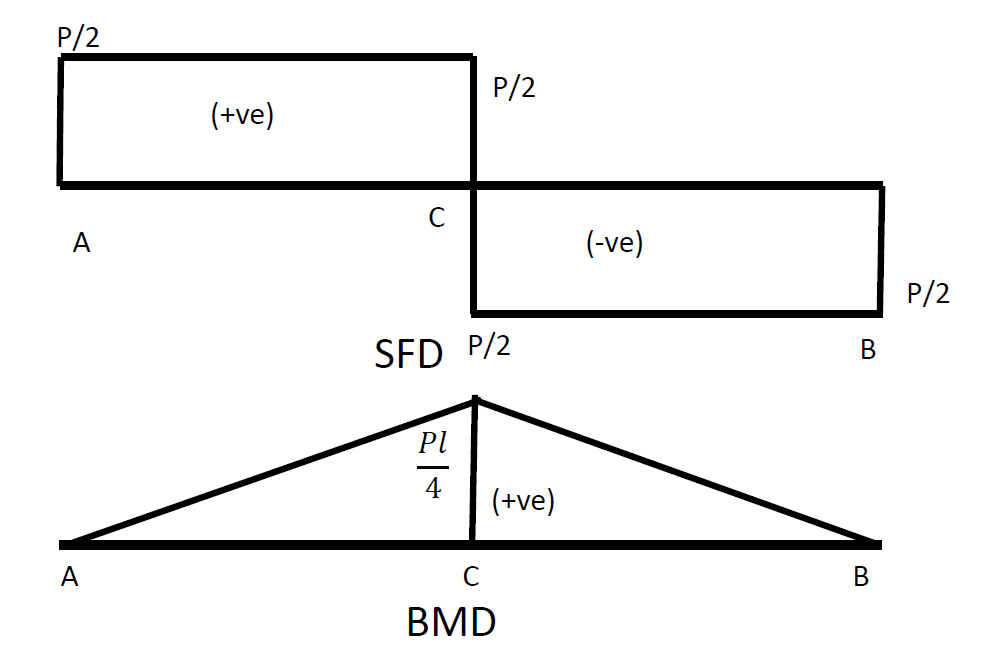
So the section of beam at point C will be subjected to maximum bending moment which means maximum bending stress.

We have the flexural equation .

M/I = E/R =σ/y

Where,
M= Bending moment acting on the beam section
I=Moment of Inertia of the section
E=Modulus of elasticity of the material of beam
R= Radius of curvature made by deflected shape of beam
σ=Bending stress 
y=Distance of extreme fiber from the neutral axis of beam
  = d/2 in case of rectangular or square beam

Now,

σ=(M/I)*y

Here,
M=Pl/4
I=bd3/12
y=d/2

σ= (Pl/4)*(d/2)/(bd3/12)

Now , the final formula for 3 point bending of a rectangular section is ,

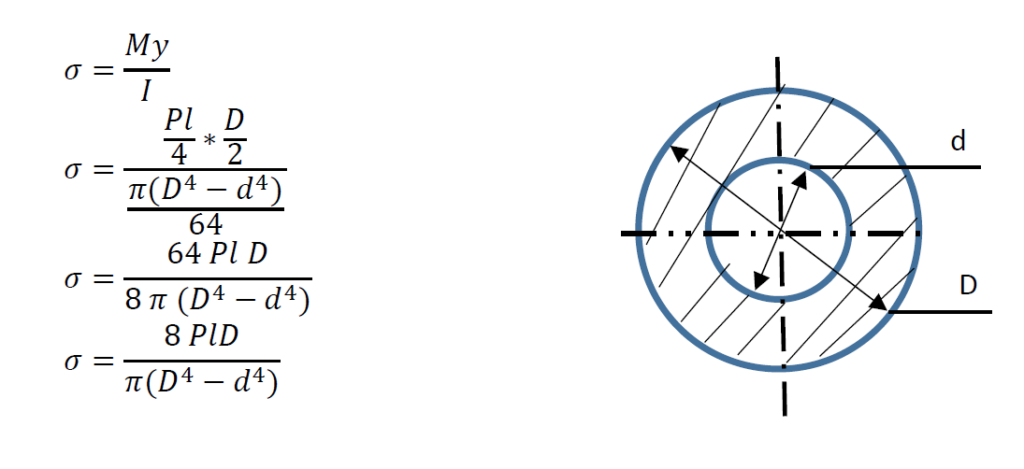
3 point Bending Formula for Circular Section

In the similar way as in for Rectangular section the formula for circular section can be derived as below.

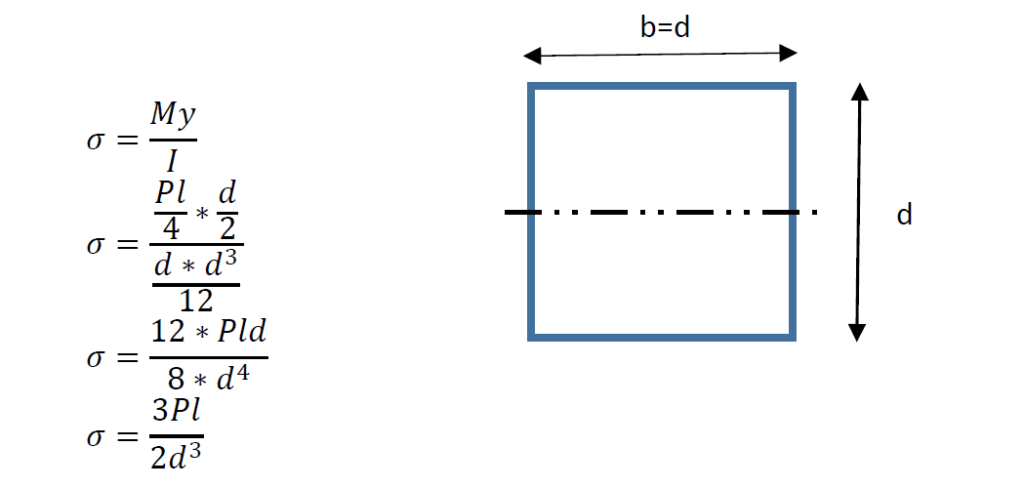
3 point Bending Formula for Square Section

In the same way as in for Rectangular section the formula for square section can be derived as below.

Three point Bending Formula for Hollow Section